DCF Method | Discounted Cash Flow Method | Value
With the DCF method, you calculate the value of a company. An example.
What is the DCF method? To discuss the more advanced methods for business
valuation, we first need to introduce the DCF method (Discounted Cash Flow method) here. The DCF method is a
commonly used technique to determine the value of a startup or a larger company by looking at the cash flow in the future.
On the page about discount rate: the present value of future money, we have seen when calculating
interest income, the future value of a certain amount grows by a factor (1 + r)n. However, a more
common question is what the value is of several amounts that will be paid out on different future dates. The DCF method
can help with that.
Using the formula above, we have calculated how much a future amount to be received in a certain period n is worth in
"today's money," namely:
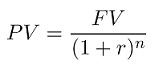
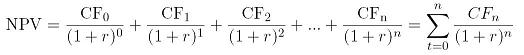
So, this is the DCF method, or discounted cash flow method, and it is the most important of all methods for a financial analyst. This method is therefore also important for those who want to evaluate an invention, and that is why we will go into detail here and illustrate how you can easily calculate an NPV with a spreadsheet.
Looking at the formula above, we see that there are a number of unknowns that we need to know before we can apply the formula, namely the cash flows (CF 0 to CF n ) and the discount rate r. We start with the latter.
Capital Asset Pricing Model and the discount rate r
So far, we have taken the discount rate, r, as interest and chosen it to make calculations easier. However, it becomes much more difficult to figure out what value to take for r when valuing a company. Before we proceed, we need to define what r actually represents.
We can illustrate this with the NPV formula. Suppose you receive two proposals.
Proposal 1 is to deposit $100 for five years in an account at a well-known bank on the corner of the street at an interest rate of 4%. So, you receive four interest payments of $4 each and a payment of $104 in year five ($4 + the invested amount, $100, also known as the principal).
Proposal 2 is to invest the same amount in a biotechnology company. In return, you receive $7 for four years and in year five, $107. Which proposal would you choose?
At first glance, this seems like an easy question to answer, and you're inclined to go with proposal 2; after all, you get more money for the same investment. But is this really the case, and how can we find out? The answer is provided by the Capital Asset Pricing Model (CAPM). CAPM is one of the most important cornerstones of finance and is used to calculate the required return for a specific investment in a particular project or company (on another page you can read more information about return and its definitions). It is calculated using the following formula:
where
- r i is the discount rate or required return, also known as cost of capital or expected return, for a specific investment, project, company, etc. We will use these terms interchangeably.
- R f is the risk-free rate.
- R m is the return of the (market) portfolio, and
- βi is the risk associated with a specific company, project i, etc.
In the following page about the Capital Asset Pricing Model (CAPM), we will continue to answer the question of whether you should invest your money in the bank or in a risky biotechnology company.
