Net Present Value (NPV) calculation
By calculating the Net Present Value, you determine whether it is worthwhile to invest in a company, business idea, or invention

The Net Present Value (NPV) is often used to determine whether it is worthwhile to invest in a startup company with an invention or a good idea. By calculating the Net Present Value, the current value of future cash flows is essentially determined, known as discounting. This allows us to determine whether added value can be created by making a certain investment now. In other words: does the investment yield sufficient returns? In the example given below, the NPV formula used is built into most spreadsheet software.
Calculating Net Present Value with a Spreadsheet
The most common and highly recommended way to calculate Net Present Value is with a spreadsheet. Most spreadsheets have built-in functions including the most common financial ones like NPV. The most well-known and widely used spreadsheets are Microsoft Excel, Numbers (Mac OS X), and OpenOffice or NeoOffice. The latter two can be downloaded and used for free. For those of you not yet familiar with a spreadsheet, now is the time to learn, because when you need to write a 'business plan,' a spreadsheet is definitely a necessity.
For the following examples, I used NeoOffice. NeoOffice is specially developed for Mac OS X, almost identical to OpenOffice, and, as mentioned earlier, free to use. It should also be noted that OpenOffice and NeoOffice can read and write Word and Excel files. Highly recommended.
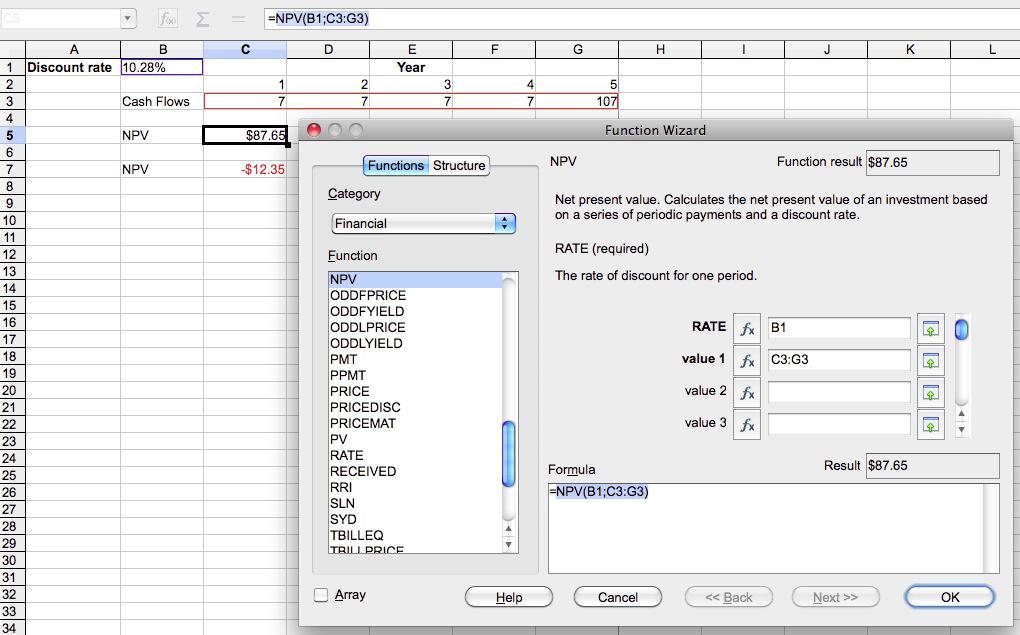
The NPV calculated with NeoOffice for Mac OS X
Calculating the Net Present Value
To calculate the NCW, we need the cash flow data and the discount rate. We know the cash flow because it was given in the example on the page about the DCF method ($7 for the first four years and $107 for the fifth year). We look up the discount rate (conveniently) in the table on the page about the Capital Asset Pricing Model and see that for a biotechnology company it is 10.28%.
The formula for the NPV in NeoOffice is = NPV(discount rate; cash flows), or in our case with the discount rate, r, in cell B1 and the cash flows (CF1 through CF5) in cells B3 through H3, = NPV(B1;C3:G3).
You can approach the NPV in two ways: with or without including the initial investment CF0 in the calculation. We will look at both:
1. NPV calculation without CF0 (the amount to be invested):
In cell C5, the NPV of the cash flow streams is calculated. The result in cell C5 is $87.65.
2. With CF0 (the amount to be invested):
In cell C7, the NPV is calculated, and we have included the negative cash outflow of $-100 as follows: NPV = -100 +
NPV(B1;C3:G3). The result in cell C7 is $-12.35.
What does this mean? This means that an investment of $100 is ultimately worth $87.65, or in other words, $12.35 less than the original investment of $100.
So every euro invested in the company will ultimately be worth $87.65. Therefore, the company is not worth much now and will be worth even less in the future than the required investment. And that is what we wanted to find out with this series about the valuation of a company. The conclusion is clear: this is not a good proposal.
Whether you show the NPV with the original investment cash outflow (CF0) or not is optional. Usually, the NPV is calculated without the cash outflow as in example 1. The result (here $87.65) is then the value of the project or company, and if this is worth less than what needs to be invested, it is a 'no go' decision. In the future, we will simply determine the value of the company with the invention included and will not include the initial amount in the NPV calculation.
Financial ratios are the figures that provide insight into how a company is performing. Knowledge of these ratios, their meaning, and how they can be applied is therefore not only important for accountants. For those who are not financially trained managers but want to make well-founded decisions about long-term strategy and short-term solutions, the book "Financial Ratios" is an absolute must.
The author of the book clearly explains what the different ratios mean and what managers need to know about interpreting them. But it doesn't just cover the theory; it also explains how ratios can be applied within a company. It also covers collaboration with managers from other departments. "Financial Ratios" is an accessible book, each chapter of which can stand alone and be read separately.
If you have worked out example (2) with a spreadsheet, try using the cash flows for the five years from example (1). For the discount rate, enter 2.5%, the interest you would receive on a five-year government bond. You will see that, if you apply the two aforementioned approaches, you will get $106.97 for NPV approach 1 and $6.97 for approach 2. This means that proposal 2 gets a positive investment recommendation, as the investment of $100 is worth $106.97.
I strongly recommend that you play around with the different parameters, e.g., increasing and decreasing the discount rate, to see the effect on the NPV. One thing is clear: the higher the discount rate (cost of capital), the lower the value, and the lower the discount rate, the more valuable the investment becomes. Incidentally, you can observe this phenomenon daily, at least if you follow financial news, because stock markets will decline when central banks raise interest rates (or the threat of this happening exists) and rise when rates are lowered. On a following page, we will take a closer look at the cash flow calculation because you need it for the valuation of your invention or business idea.
